当你看到这个标题的时候，一定很好奇，React 不是很快么？为啥会变慢呢？在写这篇文章之前，我也是这么认为的，但是当我去看了一下 React 有关 Array 的 Diff 之后，我才认识到其实 React 如果你用的不正确，那么是会变慢的。

React Diff 算法

React Diff 算法相信大家不是很陌生吧，这里就不具体展开讲了。不过有一点要补充下，Diff 算法针对的是整个 React 组件树，而不仅仅是 DOM 树，虽然这样性能会比较低一些，但是实现起来却很方便。

而在 Diff 算法中，针对数组的 diff 其实是比较有意思的一个地方。在开始讲解方面，我希望你能对 React 有一定的了解和使用。

试一试有什么区别？

首先我们创建 3 个组件，分别渲染 10000 个 DOM 元素，从 [1...10000] ，渲染成如下。

1
2
const e10000 = new Array(10000).fill(0).map((_, i) => i + 1)
element10000.map(i => <div key={`${i}`}>{i}</div>)

每个组件有两个状态，会切换数据的顺序

  • 组件 A 在 [1...10000] 和 [2,1,3...10000] 之间切换。

  • 组件 B 在 [1...10000] 和 [10000,1...9999] 之间切换

  • 组件 C 在 [1...10000] 和 [10000...1] 之间切换，也就是正序和倒序之间切换。

我们简单命名下，默认的初始状态为 S1 而切换之后的状态为 S2 。大家可以思考一下，同一个组件状态切换的时候，所耗费的时间是不是都是一样的？可以直接使用这个 DEMO。

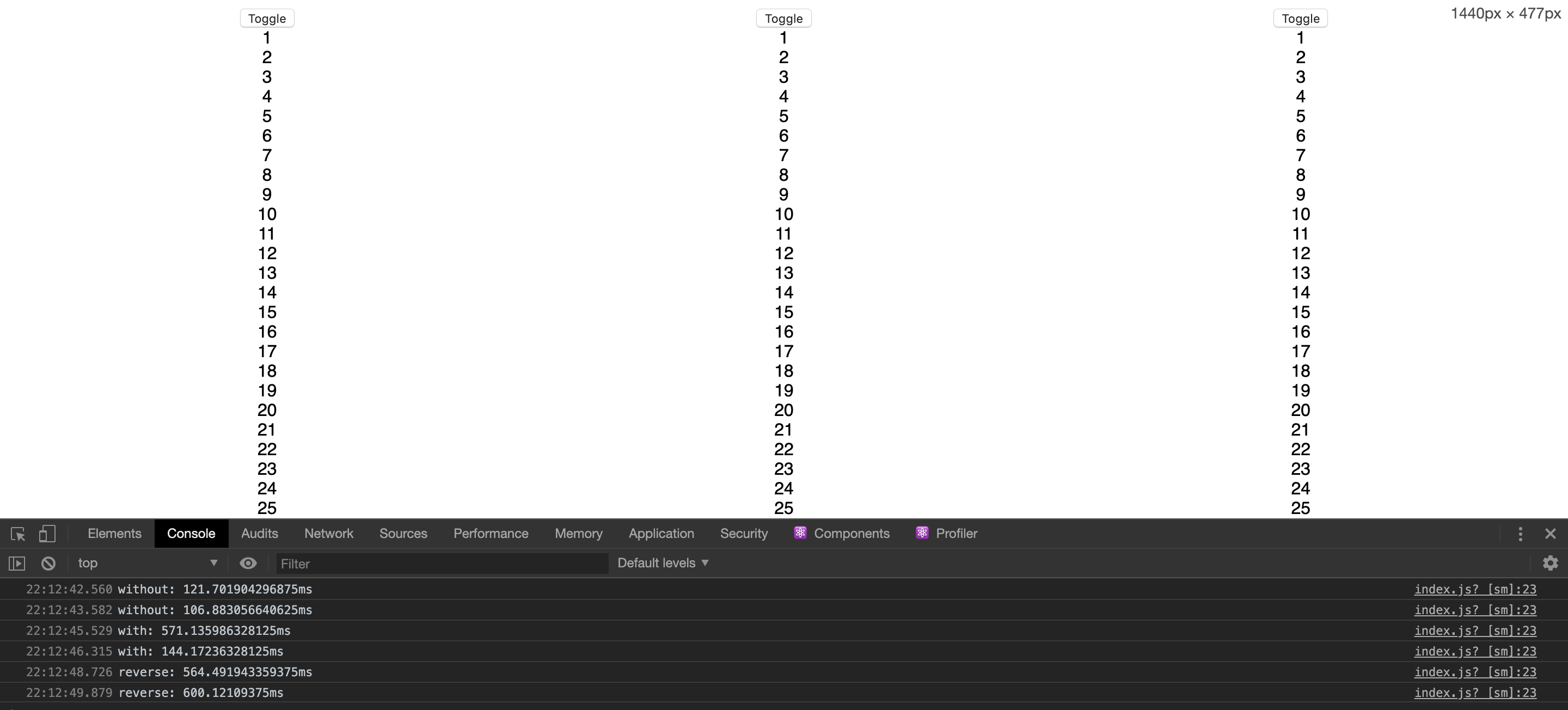
可以直接点击上方的 toggle 来切换两者之间的状态，并在控制台中查看渲染的时间。因为每次时间都不是绝对准确的，所以取了多次平均值，直接揭晓答案：

组件 S2 ⇒ S1 S1 ⇒ S2
A 102ms 103ms
B 129ms 546ms
C 556ms 585ms

有么有觉得很奇怪，为什么同样是 S1 ⇒ S2 ，同样是只改变了一个元素的位置，为什么 A 和 B 的时间差距有这么多的差距。这个具体原理就要从 Diff 算法开始讲起了。

Array Diff 的原理

在讲 React 的实现之前，我们先来抛开 React 的实现独立思考一下。但是如果直接从 React 的组件角度下手会比较麻烦，首先简化一下问题。

存在两个数组 A 和 B，数组中每一个值必须要保证在对应数组内是唯一的，类型可以是字符串或者数字。那么这个问题就转变成了如何从数组 A 通过最少的变换步骤到数组 B。

其实每个元素的值对应的就是 React 当中的 key。如果一个元素没有 key 的话，index 就是那个元素默认的 key。为什么要强调最少？因为我们希望的是能够用最少的步数完成，但是实际上这会造成计算量的加大，而 React 的实现并没有计算出最优解，而是一个较快解。

顺便定义一下操作的类型有：删除元素，插入元素，移动元素。

这里又要引申一个特殊点，React 充分利用了 DOM 的特性，在 DOM 操作中，你是可以不使用 index 来索引数据的。简单来讲，如果用数组表示，删除需要指定删除元素的索引，插入需要指定插入的位置，而移动元素需要指定从哪个索引移动到另一个索引。而利用 DOM，我们就可以简化这些操作，可以直接删除某个元素的实例，在某个元素前插入或者移动到这里（利用 insertBefore API，如果是要在添加或者移动到最后，可以利用 append ）。这样最大的好处是我们不需要记录下移动到的位置，只需要记录下那些元素移动了即可，而且这部分操作正好可以由 Fiber 来承担。

举个例子说，从 A=[1,2,3] 变化到 B=[2,3,4,1]，那么只需要记录如下操作即可：

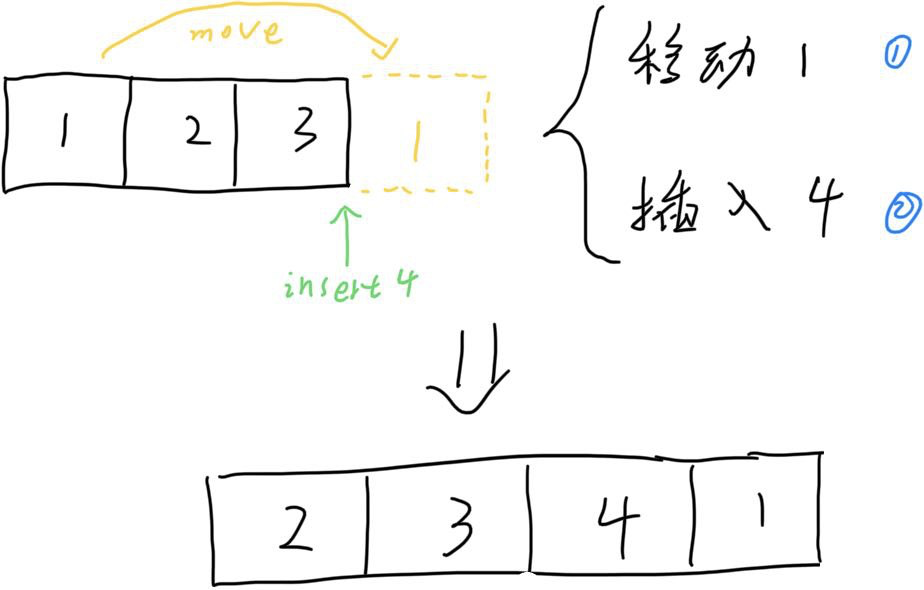
有人好奇，不需要记录移动插入到那个元素前面么？其实不需要的，这是因为你有了操作列表和 B 数组之后，就可以知道目标元素在哪里了。而且采用这种方式就根本不需要关心每次操作之后索引的变化。

回到上面的简化后的问题，首先通过对比 A、B 数组，可以得到哪些元素是删除的，哪些元素是添加的，而不管采用什么样子的策略，添加删除元素的操作次数是无法减少的。因为你不能凭空产生或者消失一个元素。那么我们问题就可以再简化一下，把所有的添加删除的元素剔除后分别得到数组 A’ 和 B’，也就是 A’ 中不包含被删除的元素，B’ 中不包含被添加的元素，此时 A’ 和 B’ 的长度一定是一样长的。也就是求解出最少移动次数使得数组 A’ 能够转化成数组 B’。

如果只是简单的求解一下最少移动步数的话，答案很简单，就是最长上升子序列（LIS，Longest Increasing Subsequence）。关于如何证明为什么是最长不下降子序列这个算法，可以通过简单的反证法得到。关于这个算法的内容我就不具体讲解了，有兴趣的可以自行 Google。在这里我们只需要知道这个算法的时间复杂度是 O(n^2) 。

但是现在我们还无法直接应用这个算法，因为每个元素的类型可能是字符串或者数字，无法比较大小。定义数组 T 为 B’ 内元素在 A’ 的位置。举个例子，如果 A' = ['a', 'b', 'c'] B' = ['b', 'c', 'a']，那么 T = [2, 3, 1]。本文约定位置是从 1 开始，索引从 0 开始。

此时便可以对 T 求解 LIS，可以得到 [2, 3]，我们将剩下不在 LIS 中的元素标记为移动元素，在这里就是 1，最后补上被剔除的删除和插入的元素的操作动作。这样 Diff 算法就可以结束了。

上面讲解的是一个个人认为完整的 Array Diff 算法，但是还是可以在保证正确性上继续优化。但是不管优化，这个复杂度对于 React 来讲还是偏高的，而如何平衡效率和最优解成为了最头疼的问题，好在 React 采用了一个混合算法，在牺牲掉一定正确性的前提下，将复杂度降低为 O(n)。下面我们来讲解下。

React 简化之后的 Array Diff

大家有过 React 开发经验的人很清楚，大部分情况下，我们通常是这样使用的：

  • 情形1：一个标签的的直接子子标签数量类型顺序不变，通常用于静态内容或者对子组件的更新

    1
    2
    3
    4
    5
    6
    7
    // 比如每次渲染都是这样的，里面的直接子元素的类型和数量是不变的，在这种情况下，其实是可以省略 key
    <div>
    	<div key="header">header</div>
    	<div key="content">content</div>
    	<div key="footer">footer</div>
    	<SubCmp time={Date.now()}/>
    </div>

  • 情形2：一个标签有多个子标签，但是一般只改变其中的少数几个子标签。最常见的场景就是规则编辑器，每次只在最后添加新规则，或者删除其中某个规则。当然了，滚动加载也算是这种。

  • 情形3：交换某几个子标签之间的顺序

  • 情形4：翻页操作，几乎重置了整个子元素

上面只是简单举了几个常见的例子，大家可以发现，大部分情况下子标签变动的其实并不多，React 利用了这个，所以将 LIS 简化成以第一个元素开始，找到最近上升子序列。简单来来讲就是从头开始遍历，只要这个元素不小于前的元素，那么就加入队列。

1
2
3
4
5
Q = [4, 1, 5, 2, 3]
// 标准算法
LIS = [1, 2, 3]
// 简化后的算法，从第一个开始，找到最近的不下降子序列即可。
LIS_React = [4, 5]

我们乍一看，这个算法不对呀，随便就能举出一个例子让这个算法错成狗，但是我们要结合实际情况来看。如果我们套回前面说的几种情况，可以看到对于情况 1,2,3 来讲，几乎和简化前效果是一样。而这样做之后，时间复杂度降低为 O(n) ，空间复杂度降低为 O(1)。我们给简化后的算法叫做 LIS' 方便后面区分。

我们将 LIS 算法简化后，配合上之前一样的流程就可以得出 React 的 Array Diff 算法的核心流程了。（为什么叫核心流程，因为还有很多优化的地方没有讲）

变慢的原因？

当我们在了解了 React 的实现之后，我们再回过来头来看看前面给出的三个例子为啥会有这么大的时间差距？

  • 组件 A 从 [1...10000] 变化到 [2,1,3...10000] 。此时我们先求解一下 LIS' 可以得到 [2,3,4...10000]，那么我们只需要移动 1 这个元素就可以了，将移动到元素 3 前面。同理反过来也是如此，也就是说 S1 ⇒ S2 和 S2 ⇒ S1 的所需要移动的次数是一致的，理论上时间上也就是相同的。

  • 组件 B 从 [1...10000] 变化到 [10000,1,2...9999] 。同理，先计算 LIS' 可以得到 [10000]，没错，你没看错，就是只有一次元素，那么我需要将剩下的所有元素全都移动到 10000 的后面去，换句话要进行 9999 次移动。这也就是为啥 S1 => S2 的时间会这么慢。但是反过来却不需要这个样子，将状态反过来，并重新计算索引，那么也就是从 [1...10000] 到 [2,3....10000,1]，在计算一次 LIS' 得到 [2,3...10000] ，此时只需要移动一次即可，S2 ⇒ S1 的时间也就自然恢复的和组件 A 一致。

  • 组件 C 是完全倒序操作，所以只分析其中一个过程即可。首先计算 LIS' 可以得到，[10000] ，也就是说要移动 9999 次，反过来也是要 9999 次，所以时间状态是一致的。

经过这样的分析大家是不是就明白为啥会变慢了吧？

优化细节

降低 Map 的生成操作次数

上面有一点没有讲到，不知道大家有没有思考到，我怎么知道某个元素是该添加函数删除呢？大家第一反应就是构建一个 Set，将数组元素全放进去，然后进行判断就可以了。但是在 React 中，其实用的是 Map，因为要存储对应的 Fiber，具体细节大家可以不用关注，只需要知道这里用 Map 实现了这个功能。

不管怎么样，根据算法，一开始肯定要构建一遍 Map，但是我们来看下上面的 情形1。发现内容是根本不会发生变化的，而且对于 情形2 来讲，有很大的概率前面的大部分是相同的。

于是 React 一开始不构建 Map，而是假设前面的内容都是一致的，对这些元素直接执行普通的更新 Fiber 操作，直到碰到第一个 key 不相同的元素才开始构建 Map 走正常的 Diff 流程。按照这个方式，情形1根本不会创建 Map，而且对于情形2、3来讲也会减少很多 Map 元素的操作（set、get、has）。

降低循环次数

按照上面的算法，我们需要至少 3 遍循环：第一遍构建 Map，第二遍剔除添加删除的元素生成 A’ 和 B’，第三遍计算 LIS 并得到哪些元素需要移动或者删除。而我们发现第二遍和第三遍是可以合并在一起的。也即是说我们在有了 Map 的情况下，不需要剔除元素，当遍历发现这个元素是新增的时候，直接记录下来。

总结

关于 Diff 算法其实还有很多的细节，我这边没有过多讲解，因为比较简单，比较符合直觉。大家有兴趣的可以自己去看下。另外有人应该会注意到，上面的例子中，为什么切换同样的次数，有的时间长，有的时间短了。日后有时间再分析下补充了。